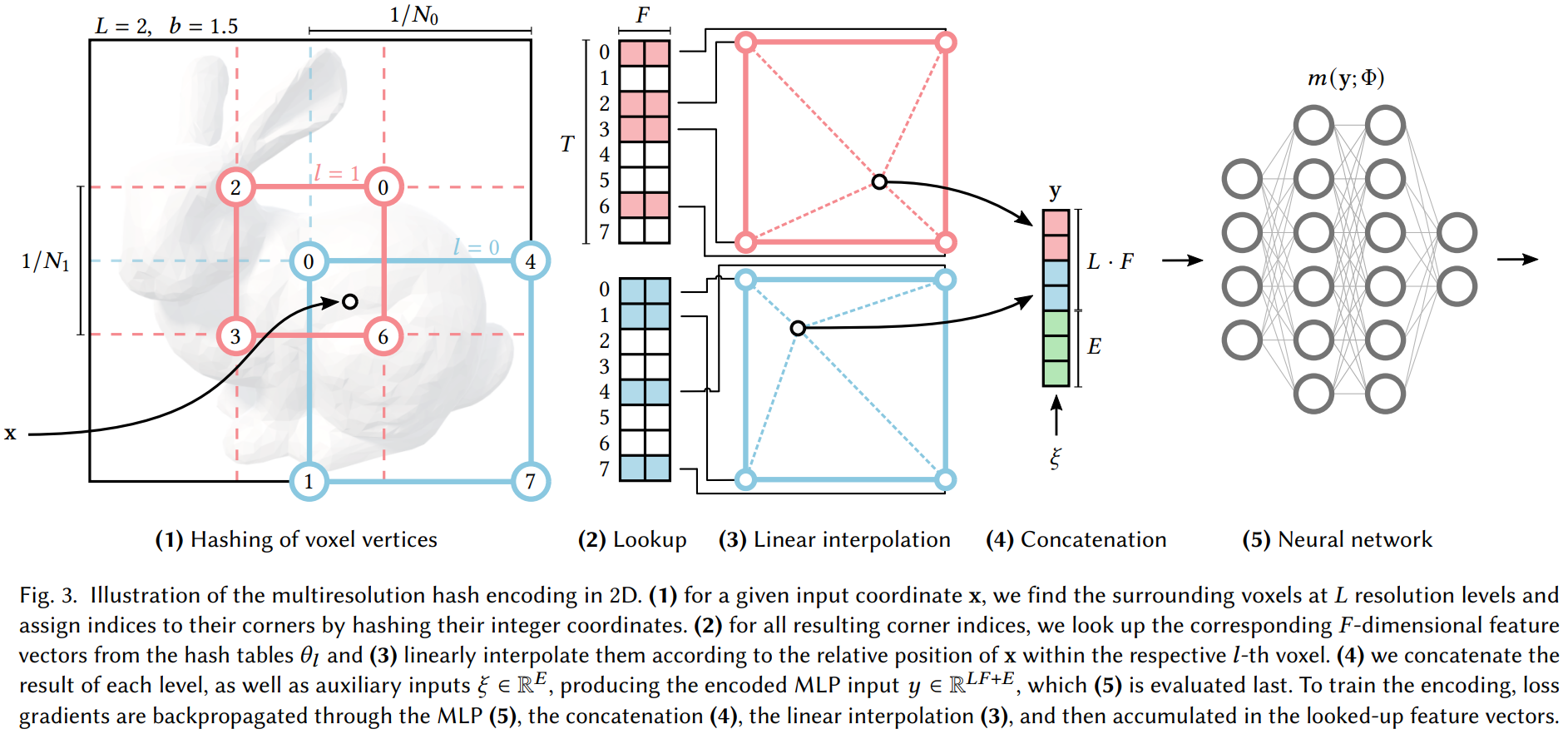
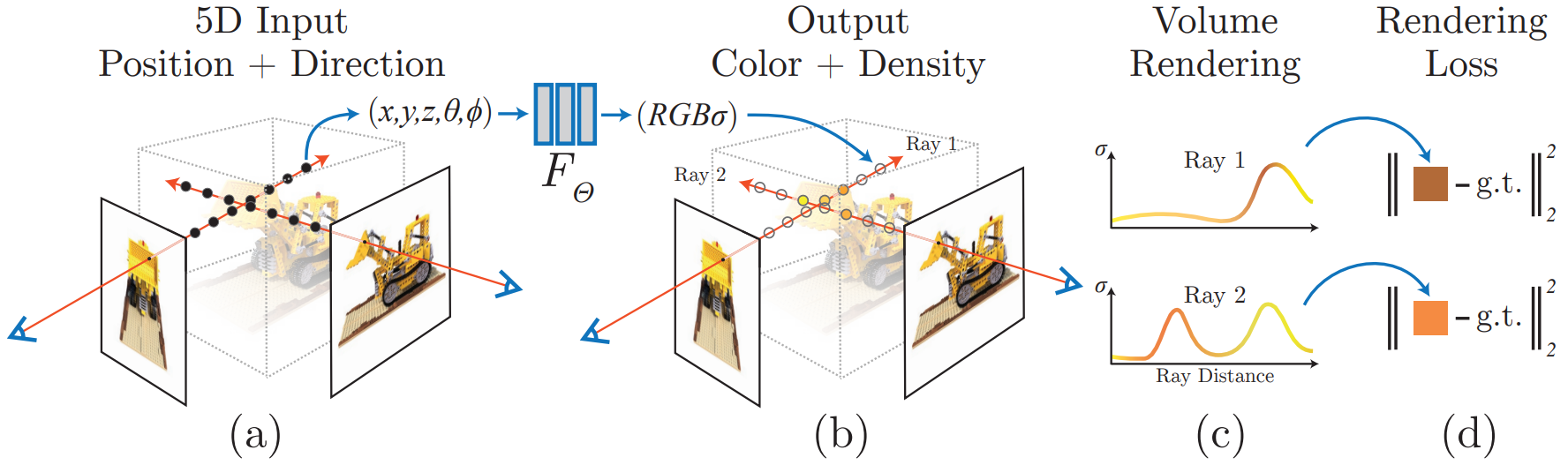
NeuS

NeuS项目主页：NeuS: Learning Neural Implicit Surfaces by Volume Rendering for Multi-view Reconstruction

Motivation

• 本文目的：从多视角2D图片，重建物体的3D表面。
• 传统的神经表面重建工作（DVR，IDR）要求前景 mask 做监督，并且容易陷入局部最小值，因此难以重建具有自遮挡或薄结构的物体；
• 对 NeRF 及其变体通过深度学习生成的高质量隐式表面没有足够的表面限制，难以提取高质量表面。

Contribution

• 提出了一种新颖的神经表面重建方法——NeuS（Neural surface Reconstruction）：将表面表示为符号距离函数（SDF： signed distance function）的零水平集（zero-level），通过新式的体渲染（volume rendering）方法来训练 SDF 表示；
• 相对于传统体渲染方法，提出一种在一阶估计中无偏的公式，达到更精确的表面重建甚至可以不用 mask 监督。

Input & Output

• Input： 多视角RGB图片、对应图片的相机位姿，Mask（可选）
• Output： SDF

Method

Scene representation

NeuS 是隐式表面重建，通过将待重建表面表达为 SDF 函数的零水平集，利用 MLP 和体渲染方法学习出这种神经 SDF 表示，具体场景表示建模如下：

• SDF： $f:\mathbf{x}\in\mathbb{R}^3\to signed\ distance\in\mathbb{R}$，$\mathbf{x}$ 为空间位置；

  • 默认待重建表面是水密的（密闭的）；
  • SDF 表示空间任一点到待重建表面的有向距离，当该点在物体外部时距离为正，在物体内部时距离为负，

• Logistic density distribution：$\phi_s(x)=s e^{-s x}/(1+e^{-s x})^2$；

  • 即 Sigmoid 函数 $\Phi_s(x)=1/(1+e^{-sx})$ 的导数，$\phi^\prime_s(x)=\Phi^\prime_s(x)$；
  • 事实上 $\phi_s(x)$ 可以是任意以 $0$ 为中心的单峰密度分布，这里出于计算方便；
  • 标准差为 $1/s$，也是一个可训练的参数，希望最终收敛 $1/s\sim 0$；

• 待重建的表面被表示为 zero-level 集：$\mathcal{S}={\mathbf{x}\in\mathbb{R}^3|f(\mathbf{x})=0}$；

• 密度函数 S-density：$\sigma(\mathbf{x})=\phi_s(f(\mathbf{x}))$；
• 辐射场函数 $c:(\mathbf{x,v})\in\mathbb{R}^3\times\mathbb{S}^2\to\mathbb{R}^3$，$\mathbf{v}$ 为观察方向；
  • 对空间任一点 $\mathbf{x}$，在给定观察方向 $\mathbf{v}$ 下的颜色值；

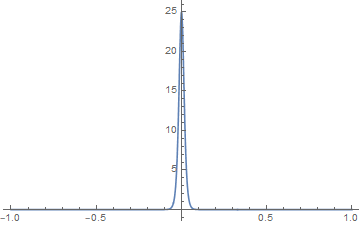
期望的是训练结果，待重建的表面SDF接近于 $0$，其他地方为有向距离；并且训练收敛后 $1/s\sim 0$，S-density $\phi_s(f(\mathbf{x}))$ 在待重建的表面附近有显著的高值，其他位置趋近于 $0$（如下图）。

Volume Rendering

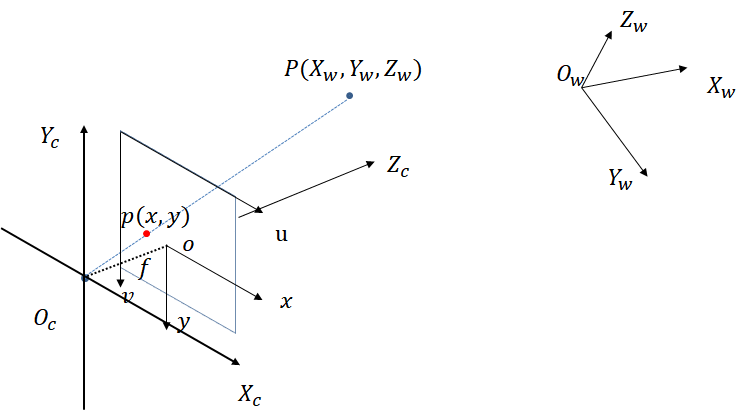
为了学习（训练）神经SDF表示和辐射场的参数，作者建议采用体渲染的方法来渲染SDF表示中的图片，所以，对任一图片内给定像素，其基于相机内部光心原点 $\mathbf{o}$ 在观察方向 $\mathbf{v}$ 发出的一条光线 ${\mathbf{x}(t)=\mathbf{o}+t \mathbf{v}|t\geq 0}$，沿光线累积颜色：

$$C(\mathbf{o,v})=\int_0^{+\infty}w(t)c(\mathbf{x}(t),\mathbf{v})d t$$

$w(t)$ 为点 $\mathbf{x}(t)$ 的权重，$C(\mathbf{o,v})$ 即为这个像素的输出颜色。

Requirements on weight function

可以说，从 2D 图片学习精确的 SDF 表示的关键就在于构建出一种输出的颜色值与 SDF 的合适的联系，也即，基于场景的 SDF $f$ 推导出一个合适的权重函数。对权重函数的要求如下：

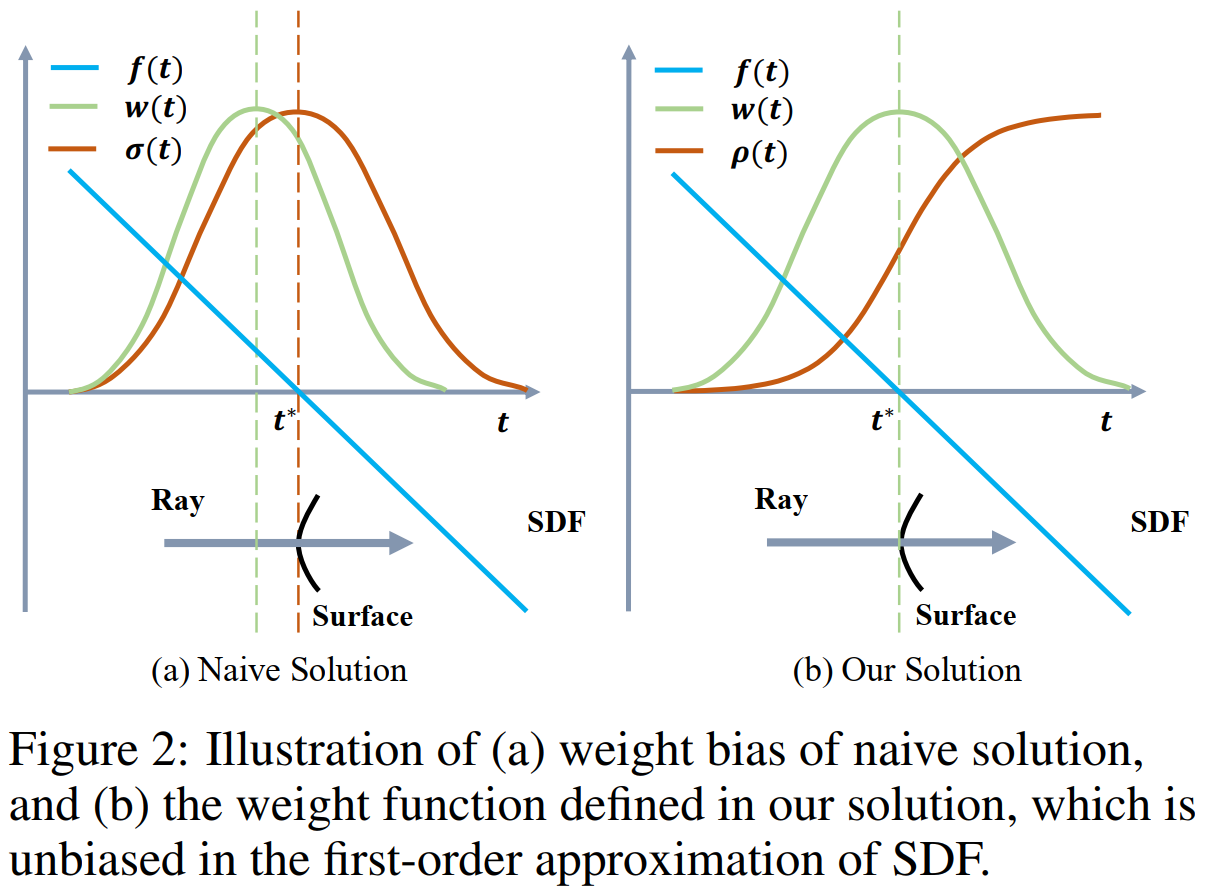
• 无偏性（Unbiased）。在光线与表面交点处 $\mathbf{x}(t^\ast)$，也即：$f(\mathbf{x}(t^\ast))=0$ 时，$w(t)$ 达到局部最大值；

  • 保证光线与表面（SDF零水平集）交点对像素颜色贡献最大；

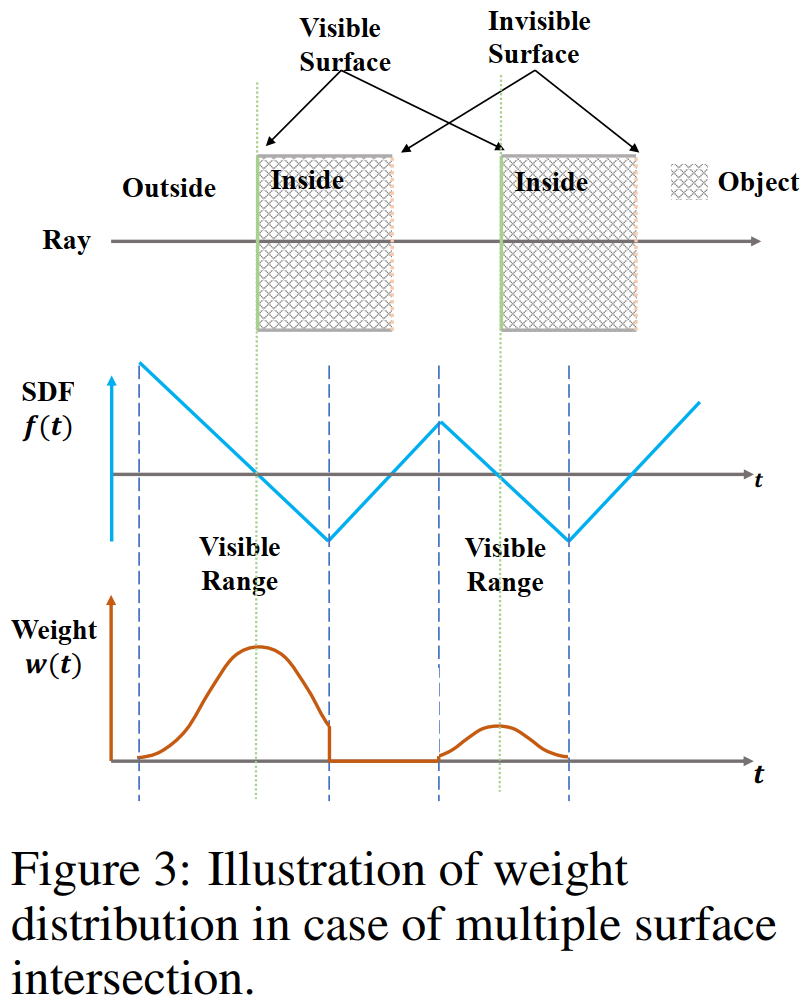
• 感知遮挡（Occlusion-aware）。

  • $$f(t_0)=f(t_1),\quad t_0<t_1,\quad w(t_0)>0,w(t_1)>0 \Rightarrow w(t_0)>w(t_1)$$

    即更靠近相机的点有更大的权重，也即对最终的输出颜色贡献更大；

  • 确保当光线依次通过多个表面时，渲染过程将正确地使用离相机最近的表面的颜色来计算输出颜色。

在传统的体渲染中：$w(t)=T(t)\sigma(t),\quad T(t)=exp(-\int_0^t \sigma(u)d u)$ 为沿光线累积透射率（accumulated transmittance），$\sigma(t)=\phi_s(f(\mathbf{x}(t)))$ 为体密度（volume density）。——遮挡感知的，但是有偏的，会在重建表面引入固有错误（如下图，在表面交点处，权重函数并没有局部最大）。

**NeuS的方案。** $$ \begin{aligned} w(t)&=T(t)\rho(t),&\cdots(1)\\ T(t)&=exp\left(-\int_0^t \rho(u)d u\right),&\cdots(2)\\ \rho(t)&=\max\left(\frac{-\frac{d\Phi_s}{dt}(f(\mathbf{x}(t)))}{\Phi_s(f(\mathbf{x}(t)))},0\right).&\cdots(3) \end{aligned} $$ 其中式子 (1) 为传统体渲染格式，保证了遮挡感知；式子 (3) 为不透明密度（opaque density）函数。这在 SDF 的一阶近似中是无偏的（具体推导参见论文即可，无偏的示例如上面图2b所示，多表面交点示例如下所示）。

Discretization

为了对不透明密度和权重函数的离散化形式，采用类似 NeRF 中的同样的估计方法。沿光线采样 $n$ 个点，从而沿此光线的像素处颜色为 ：

$$\begin{aligned} \hat{C}&=\sum_{i=1}^n T_i\alpha_i c_i \\ T_i&=\prod_{j=1}^{i-1}(1-\alpha_j) \\ \alpha_i&=max\{\frac{\Phi_s(f(\mathbf{x}(t_i)))-\Phi_s(f(\mathbf{x}(t_{i+1})))}{\Phi_s(f(\mathbf{x}(t_i)))},0\}. \end{aligned}$$

有关 $\alpha_i$ 的详细推导参见原文的附录。

Training

通过在每次迭代中，从一张图片内随机的选取一部分（batch）像素以及世界空间 $P={C_k,M_k,\mathbf{o}_k,\mathbf{v}_k}$ 内相应的光线来优化神经网络和上述标准差的倒数（$1/s$），其中 $C_k$ 为像素的真实颜色，$M_k\in{0,1}$ 为可选的 Mask 的值，即是否有 Mask。$n$ 为采样点数，$m$ 为 batch size。

• 损失函数：

  $$\mathcal{L}=\mathcal{L}_{color}+\lambda\mathcal{L}_{reg}+\beta\mathcal{L}_{mask}$$

  • 光度（颜色）损失：

    $$\mathcal{L}_{color}=\frac{1}{m}\sum_k\left|\hat{C}_k-C_k\right|$$
    • 监督渲染颜色接近真实值颜色

  • Eikonal loss：

    $$\mathcal{L}_{reg}=\frac{1}{nm}\sum_{i,k}\left(\parallel\nabla f(\hat{\mathbf{x}}_{k,i})\parallel_2-1\right)^2$$

    • 约束 MLP 学习出的 SDF 的导数满足导数模长等于 1 的性质；

    • 简单证明：

      假设上述 $f$ 是定义在 $\Omega\in\mathbb{R}^3$ 上的 SDF，

      对 $\forall \mathbf{x}\notin\partial\Omega$，存在一个最近点 $\mathbf{y}\in\partial\Omega$，

      因此 $\mathbf{v}=(\mathbf{y-x})/\parallel\mathbf{y-x}\parallel$ 是最速下降方向，也即与 $\nabla f(\mathbf{x})$ 同向，

      又因 $f$ 定义，即恰好表示其到最近点的距离，

      故沿 $\mathbf{v}$ 方向移动一单位，$f$ 也变化一单位，

      即方向导数满足 $D_v f=\nabla f(\mathbf{x})\cdot\mathbf{v}=\parallel\nabla f(\mathbf{x})\parallel\parallel\mathbf{v}\parallel\cos\theta=1$，

      故 $\parallel\nabla f\parallel=1$。

  • 可选的掩码损失：

    $$\mathcal{L}_{mask}=BCE(M_k,\hat{W}_k),\quad\hat{W}_k=\sum_{i=1}^nT_{k,i}\alpha_{k,i}$$
    • $\hat{W}_k$ 沿相机光线的权重总和，$BCE$ 是二元交叉熵损失。

• 分层采样（Hierarchical sampling）：

  • 首先沿射线均匀采样 64 个点，然后迭代进行 $k=4$ 次的重要性采样。
  • 只维护一个网络（不像NeRF中同时维护粗糙和精细两个网络）
    • 粗采样的概率基于固有标准差的 S-density $\phi_s(f(\mathbf{x}))$ 计算；
    • 精细采样的概率则是基于学习到的 $s$ 的 $\phi_s(f(\mathbf{x}))$ 计算；
    • 具体细节参见原论文附录以及渲染代码。