Motivation

本文目的：新视角合成（new view synthesis），对输入的 2D RGB 多视角稀疏图片，合成其他视角下的高逼真图片。

Contribution

提出了一种可以应对复杂几何和材质的连续场景的表示方法 NeRF：参数化为 MLP 的神经辐射场；
基于经典体渲染技术的可微渲染过程，提出分层采样策略，充分利用 MLP 的表达能力以对网络进行优化；
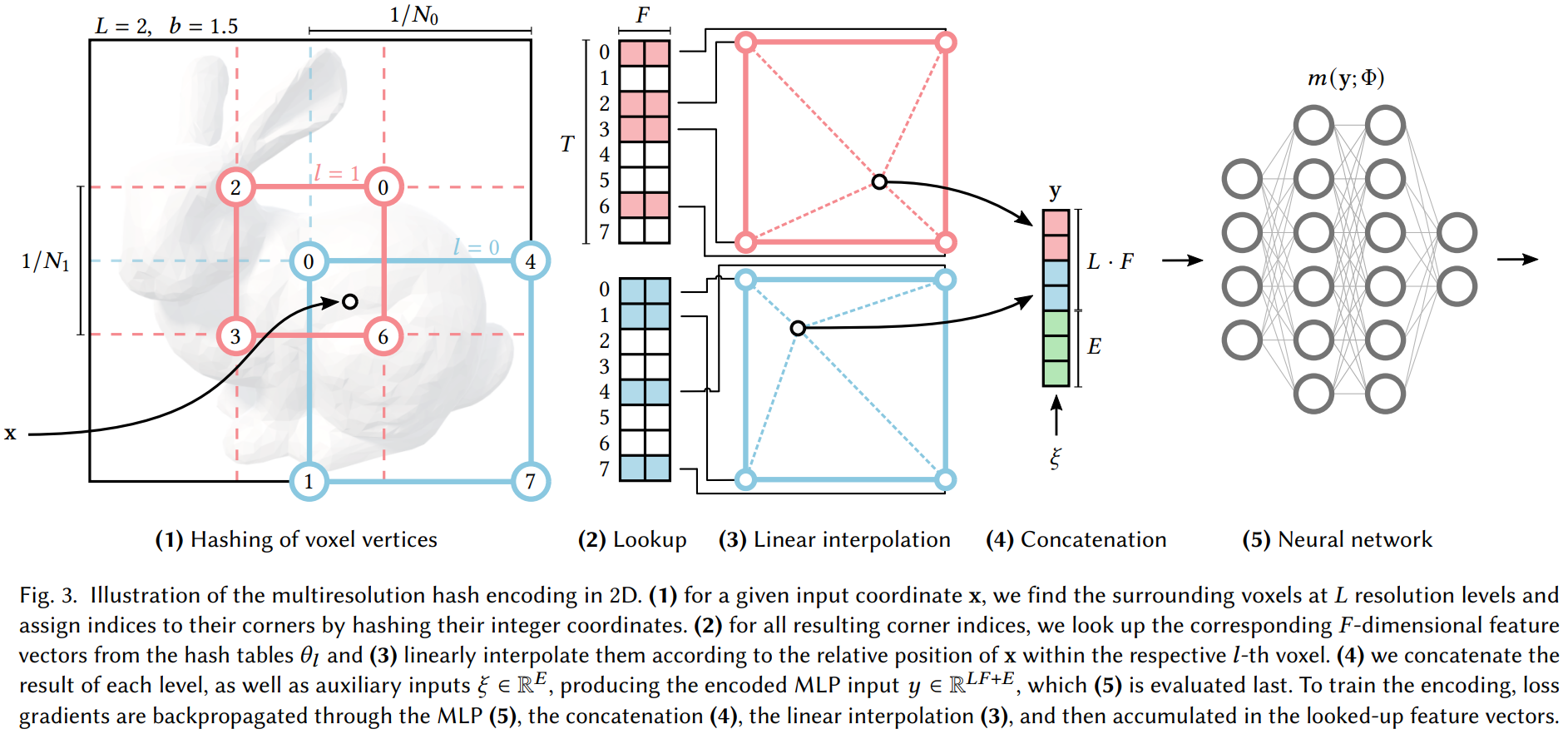
使用位置编码（Position Encoding），将输入的 5D 坐标映射到更高维的空间，让 NeRF 可以表示高频场景内容。

Input & Output

Input： 多视角RGB图片、对应图片的相机位姿;
Output： NeRF 场景表示

Introduction

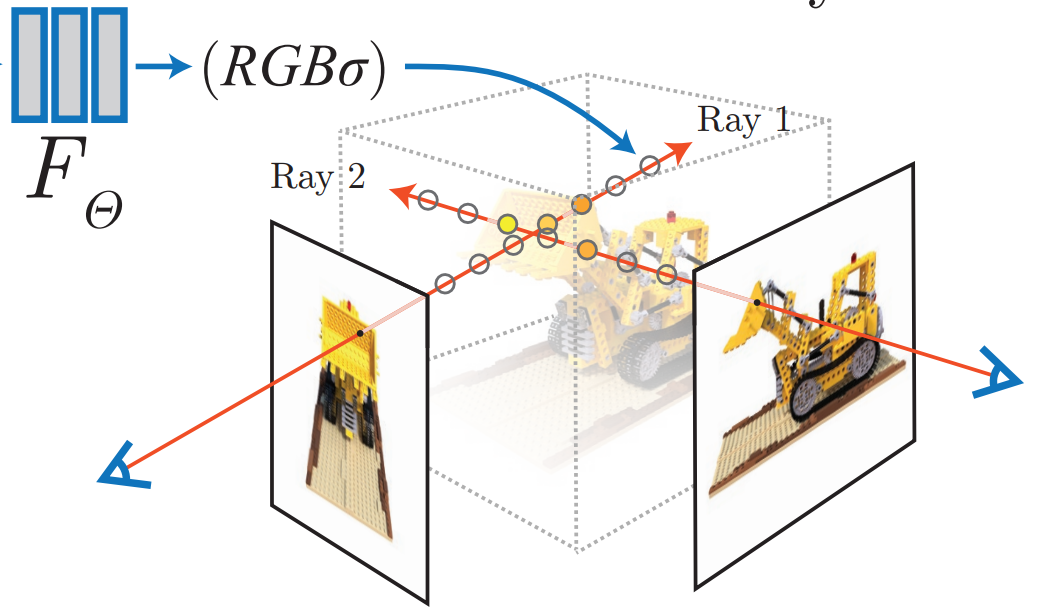
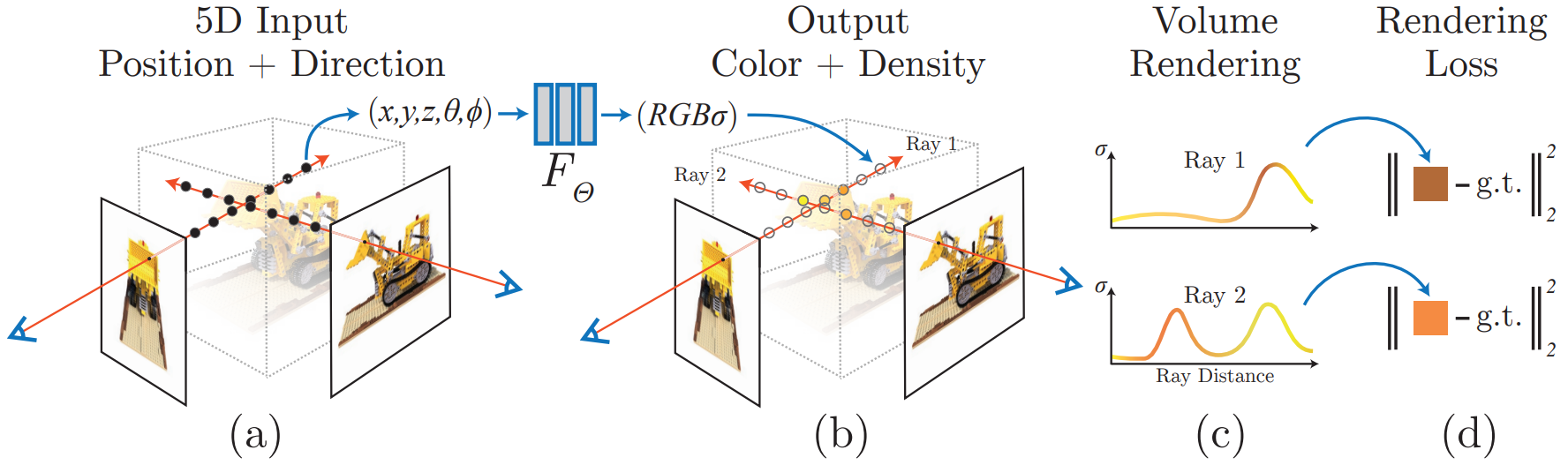
本文以一种新颖的方式解决了长期存在的视图合成问题：将静态场景表示（拟合）为连续的 5D 函数，函数输出各个空间点 $\mathbf{x}=(x,y,z)$ 在各个方向 $\mathbf{v}=(\theta,\phi)$ 的辐射亮度（颜色）和密度；通过优化一个（无卷积层）深度全连接神经网络（MLP，多层感知器，multilayer perceptron）的参数，根据一个 5D 输入 $(x,y,z,\theta,\phi)$，最小化渲染图像与真实图像的误差损失，回归学习输出空间该点处的体密度和此方向下的 RGB 颜色。流程图（Pipeline）如下：

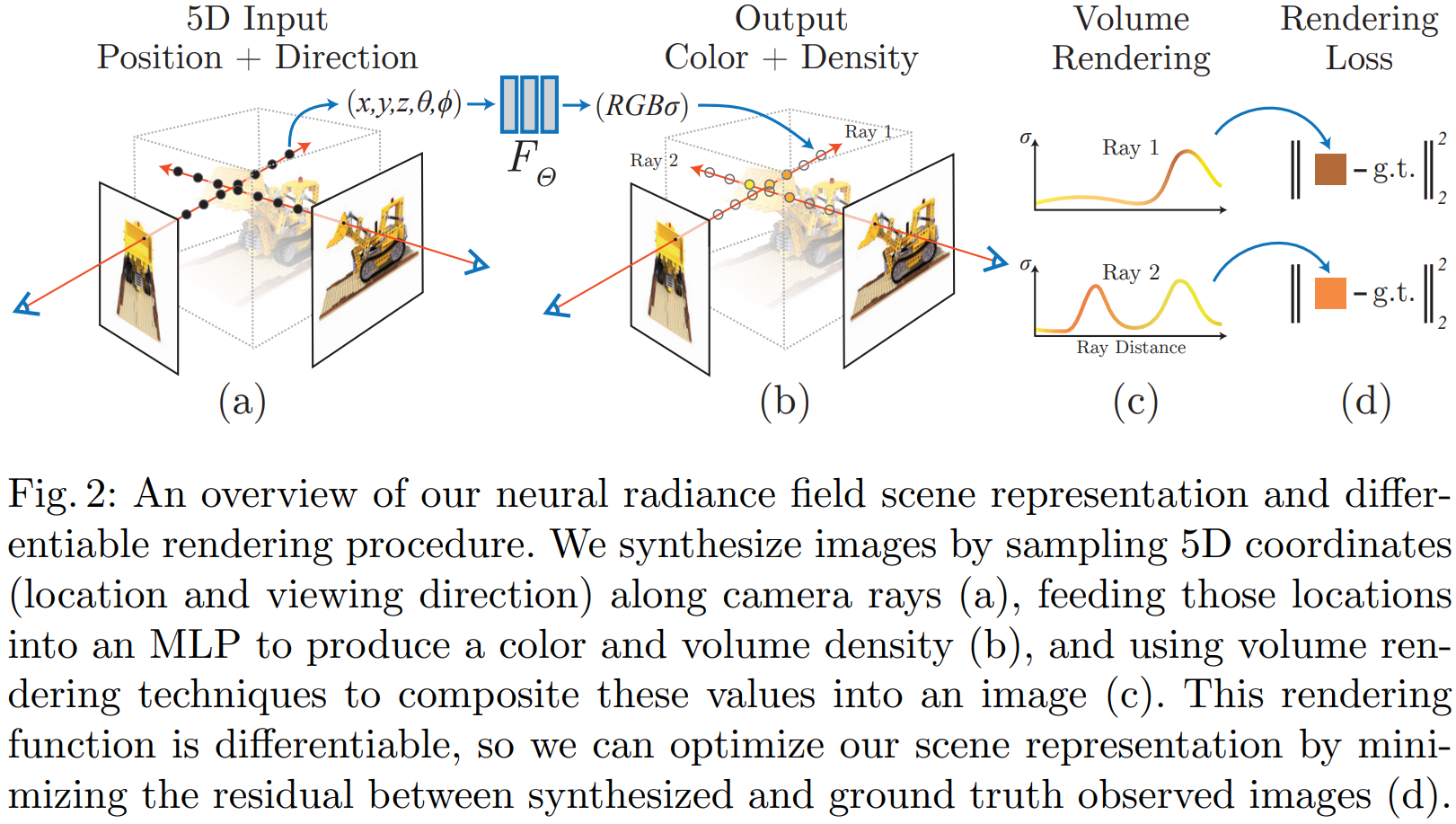
Neural Radiance Field Scene Representation

NeRF 通过将一个连续的静态场景表示为一个 5D 的向量值函数：

$F_\Theta:(\mathbf{x},\mathbf{v})\in\mathbb{R}^5\to(\mathbf{c},\sigma)$

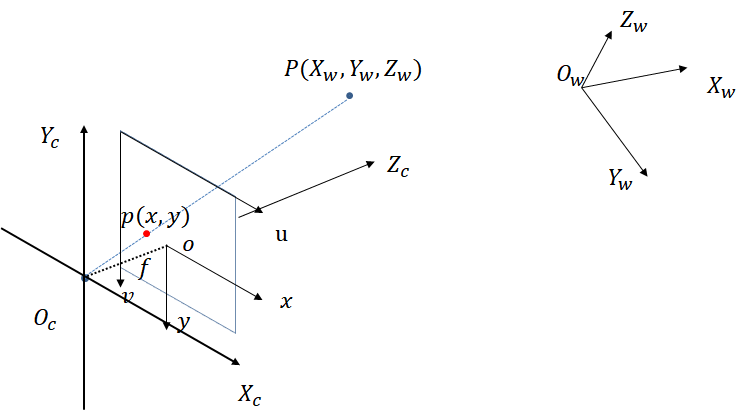
函数输入为：3D 空间位置 $\mathbf{x}=(x,y,z)\in\mathbb{R}^3$ 以及 2D 视角观察方向 $\mathbf{v}=(\theta,\phi)$（一般表示为单位笛卡尔向量，3D向量，但是模长为1）；函数输出为：辐射颜色 $\mathbf{c}=(r,g,b)$ 和空间体密度 $\sigma$。

为了将输出的依赖关系约束为：预测的体密度 $\sigma$ 仅依赖于空间位置 $\mathbf{x}$，RGB 颜色 $\mathbf{c}$ 同时依赖于空间位置 $\mathbf{x}$ 和视角方向 $\mathbf{v}$，（这是合理的，因为空间中任一点的密度不会随观察角度的变化而发生改变，但是颜色则会依赖从那个观察方向观看），以此通过这种依赖关系约束网格学习到场景的多视角连续表示，网格的具体进程如下：
- 首先使用 8 层的全连接层（ReLU 作为激活函数，每层有 256 个通道），输入 3D 空间坐标 $\mathbf{x}$，输出体密度 $\sigma$ 和一个 256 维的特征向量 $\xi$；
- 其次将上述特征向量 $\xi$ 和视角方向 $\mathbf{v}$ 连接起来作为输入，输入到另一个全连接层（ReLU 作为激活函数，每层有 256 个通道），输出和方向相关的 RGB 颜色 $\mathbf{c}$。
（后面的工作已证明这是两个独立的网络）

Volume Rendering with Radiance Fields

使用经典体渲染技术可以渲染出任意射线穿过场景的颜色。体积密度 $\sigma(\mathbf{x})$ 可以解释为：光线在位置 $\mathbf{x}$ 处终止于无穷小粒子的可微概率。在最近 $t_n$ 与最远 $t_f$ 边界的条件下，相机光线 $\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$ 的颜色 $C(\mathbf{r})$ 为：

$C(\mathbf{r}) = \int_{t_n}^{t_f} T(t)\sigma(\mathbf{r}(t))c(\mathbf{r}(t),\mathbf{d}) dt, \qquad where\quad T(t)=e^{-\int_{t_n}^{t}\sigma(\mathbf{r}(s))} ds$

其中函数 $T(t)$ 表示沿着光线从 $t_n$ 到 $t$ 所累积的透明度（accumulated transmittance），即光线从 $t_n$ 到 $t$ 未击中任何粒子的概率。视图渲染即需估计积分 $C(\mathbf{r})$，即光线通过每个像素所累积的颜色。

通过数值离散积分估计上述累积颜色：将 $[t_n,t_f]$ 区间 $N$ 等分，对每个区间段随机均匀采样，故第 $i$ 个采样点为

$t_i \sim \mathcal{U} [t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)]$

此时积分的离散形式为：

$C(\mathbf{r}) = \sum_{i=1}^{N} T_i \cdot (1-e^{-\sigma_i \delta_i}) \mathbf{c}_i,\quad where\ T_i=exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j), \quad \delta_i=t_{i+1}-t_i$

Optimizing a Neural Radiance Field

如果只是采用上述这种策略来拟合场景，对于一些复杂的场景效果并不理想，一方面很难得到较高分辨率的结果，无法恢复场景中的高频细节，另一方面不能高效利用每条光线的采样点。所以论文提出了两个进一步的优化技巧：位置编码（Position Encoding）、分层采样（Hierarchical Sampling）。

Position Encoding

Rahaman 等人证明了深度网络倾向于学习到低频函数；使用高频函数把输入映射到更高维的空间中，再传递到神经网络，可以更好地拟合具有高频变化的数据。

因此为了拟合场景中的高频细节，应用到 NeRF 中，重建的网络表示为两个函数的复合形式：

$F_\Theta \to F_\Theta=F_\Theta^\prime\circ\gamma$

其中 $F_\Theta^\prime$ 是普通的MLP，编码函数 $\gamma:\mathbb{R}\to\mathbb{R}^{2L}$ 如下：

$\gamma(p)=(\sin(2^0\pi p),\cos(2^0\pi p),\cdots,\sin(2^{L-1}\pi p),\cos(2^{L-1}\pi p))$

该函数分别作用于空间位置 $\mathbf{x}$ 以及视角方向 $\mathbf{v}$ 的每个分量。（该论文中空间位置和视角方向分别为 $L=10,4$）

Hierarchical volume sampling

前面提出的传统沿光线离散采样 $N$ 个点对于评估 NeRF 网络是不充分的：空白空间和遮挡区域对于渲染图片是没有贡献的，但是仍然被重复的采样评估。通过会早期体渲染工作的借鉴，论文提出了分层采样的策略来提升渲染效率：根据所期望的渲染效果，来按比例地分配采样点。所以并不是使用单个网络来表示场景，而是考虑同时优化两个网络：粗糙网络和精细网络。

首先使用分层抽样，采样第一个集合，包含 $N_c$ 个位置点，用上述 $t_i$ 与 $C(\mathbf{r})$ 方程计算粗糙网络，并根据粗糙网络的输出，沿着光线生成更明智的采样点（更偏向与体积相关的部分）。在上述粗网格下，重写颜色公式：
$C_c(\mathbf{r}) = \sum_{i=1}^{N_c} \omega_i \mathbf{c}_i,\qquad \omega_i=T_i(1-e^{-\sigma_i \delta_i})$
再归一化权重
$\hat{\omega_i}=\frac{\omega_i}{\sum_{i=1}^{N_c} \omega_i},$
这样就可以把上式颜色公式看作是沿着光线的分段连续概率密度函数(PDF)，可以粗略的估计此光线上物体的分布情况。
进一步，使用逆变换采样（inverse transform sampling），从上述分布采样出第二个、包含 $N_f$ 个位置点，并在第一个采样点集合和第二个采样点集合的并集上计算精细网络，最后利用上述 $N_c+N_f$ 个采样点计算最终的光线颜色 $C_f(\mathbf{r})$。

注：这种方法，可以分配更多的样本点在包含场景内容的区域内。它解决了与重要性抽样（importance sampling）相同的目标，但论文使用采样值作为整个积分域的非均匀离散化，而不是将每个样本视为整个积分的独立概率估计。

Implementation details

训练损失函数：
$\mathcal{L}=\sum_{\mathbf{r}\in\mathcal{R}} [\parallel C_c(\mathbf{r}) -C(\mathbf{r})\parallel^2_2+ \parallel C_f(\mathbf{r}) -C(\mathbf{r})\parallel^2_2]$
注意到上述同时也最小化了 $C_c(\mathbf{r})$ 的损失，以便粗网络的权重分布可用于在细网络中分配样本。
论文中 $N_c=64$，$N_f=128$；
使用 Adam optimizer（优化器），学习率（learning rate）从 $5\times 10^{-4}$ 指数下降到 $5\times 10^{-5}$，其他优化器参数 $\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-7}$。