说明:本文以机器学习中最基本的分类网络为背景,介绍神经网络的基本结构;基本只需要知道这些基本组成便可以着手具体的项目代码,而一些特殊的网络组成,只需遇到时自行搜索学习即可。
传统k-近邻(KNN)算法:
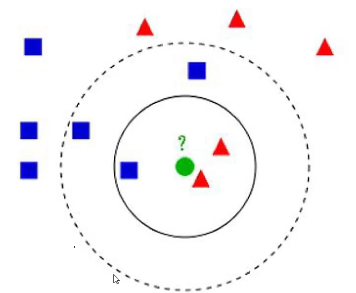
问:绿色是属于方块还是三角?——取决于 k。
算法流程:
- (1)计算已知类别数据集中的点与当前点的距离,并依次排序
- (2)选取与当前点距离最小的 k 个点,并确定类别;
- (3)返回前 k 个点出现频率最高的类别作为预测。
设计网络需要考虑
- 数据的预处理与初始化如何更高效?
- 网络结构:隐藏层层数、每层神经元个数?
- 损失函数?正则化项?
- 优化策略?
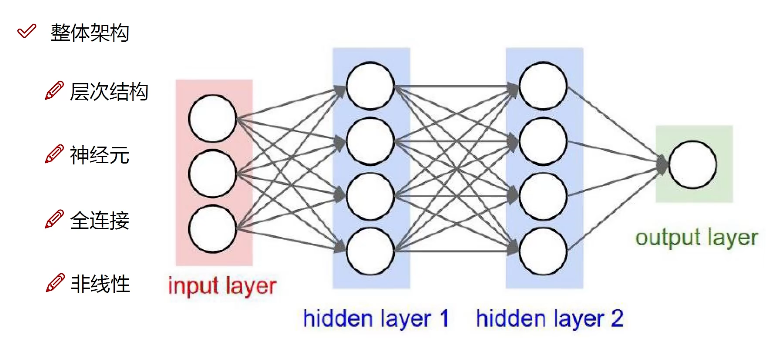
(全连接)神经网路
数据预处理和参数初始化
- 一般对输入数据进行预处理或归一化(例如映射到 $[0,1]$ 范围内),再作为网络输入;
- 对网络参数初始化时进行随机初始化(尽量浮动小一些,类似初始学习率也取很小)。
线性函数(得分函数)
假设分类有10个类别,权重和偏移分别为 $W\in\mathbb{R}^{10\times d},b\in\mathbb{R}^{10},x\in\mathbb{R}^d$,得分函数即为
相当于每个类别、每个像素点对应不同参数权重。
事实上,这个权重 $W$、偏移 $b$ 是上面网络中层与层之间连线部分计算的线性部分:从某一层输出,经过线性变换之后作为下一层的输入。
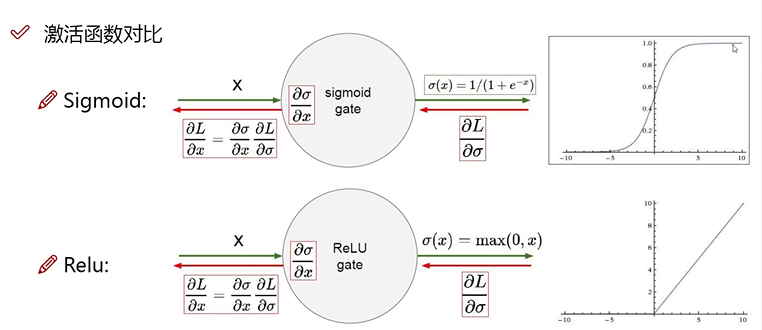
激活函数
目的:如果只是一直的线性变换,那只是简单的线性拟合,无法应对非线性数据;
方法:经过上述线性变换后,在传输到下一组神经元之前,进行非线性变换,也即激活。事实上这个激活函数就是上面每层网络中的圆圈部分。下面是两个最常用的两种激活函数:
损失函数
用于监督与反向传播,衡量计算当前得分的权重的好坏,例如这里 :
后面 $\lambda R(W)$ 为正则项,是为了削减过拟合。
$softmax$ 分类器
从而计算损失,如图中取的是交叉熵,因为概率越靠近1,损失越小。
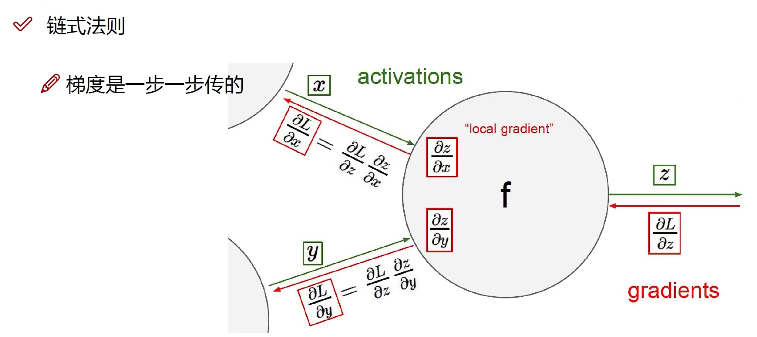
反向传播(可微)
链式法则逐层计算偏导,从网络的输出反向进行到网络的输入,以进行后续的优化,例如梯度下降法:
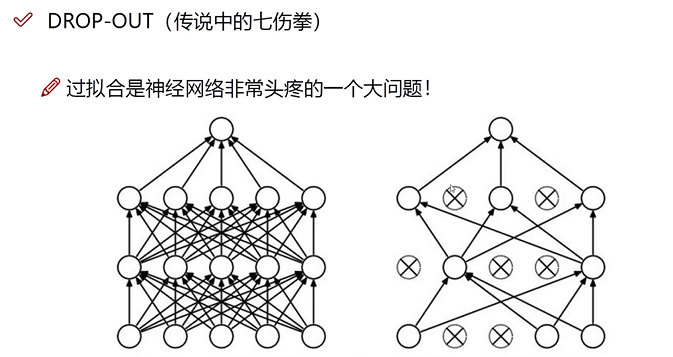
Drop-out
为了削弱过拟合部分,随机在某些训练步内失活一定的神经元:
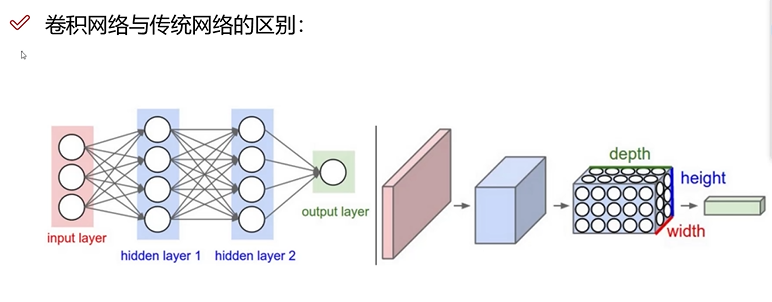
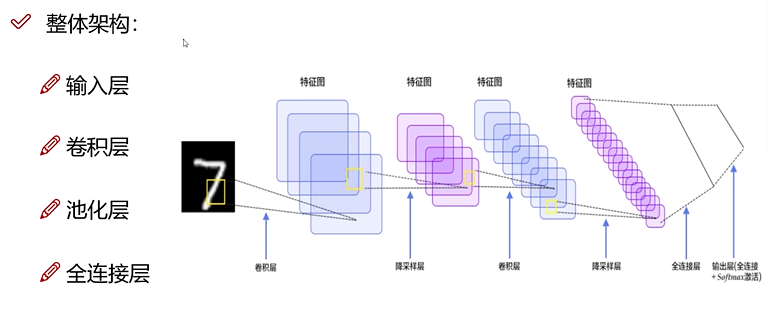
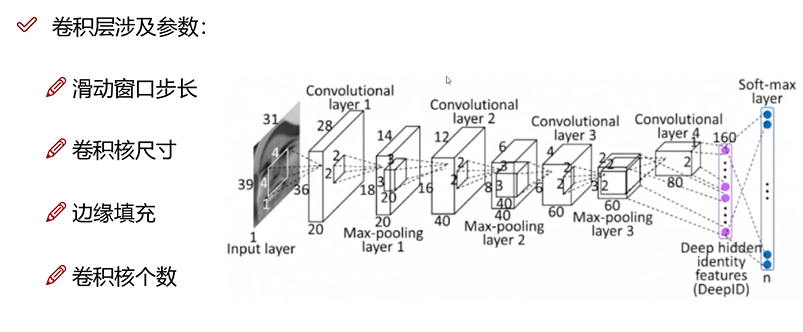
卷积神经网络
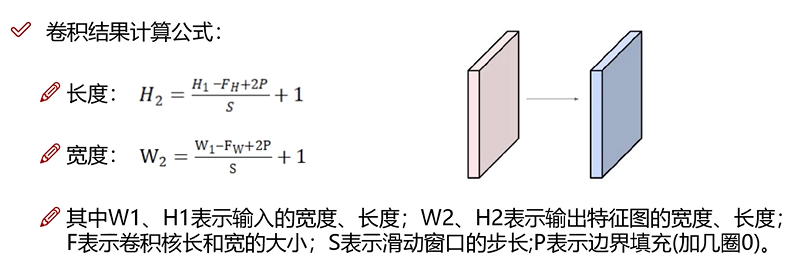
卷积层
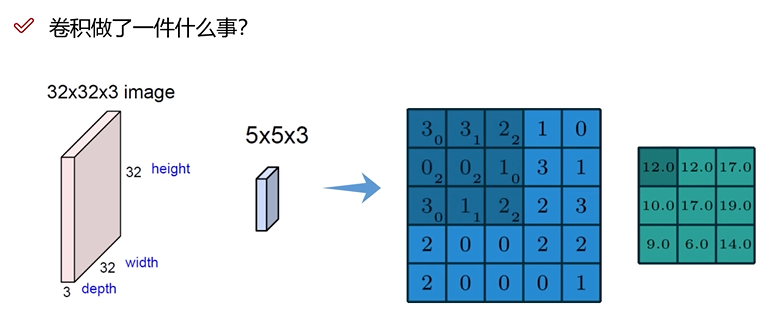
目的:增加关联性,考虑到像素与周围像素是有关联性的;
策略:利用卷积块作为权重参数对指定大小的像素块做加权组合;注意,每个颜色通道是单独做卷积。
边缘填充,是因为边界在做卷积时,边缘只计算一次,但是内部可能计算多次,为了平衡重要性,在边缘添加一圈0。
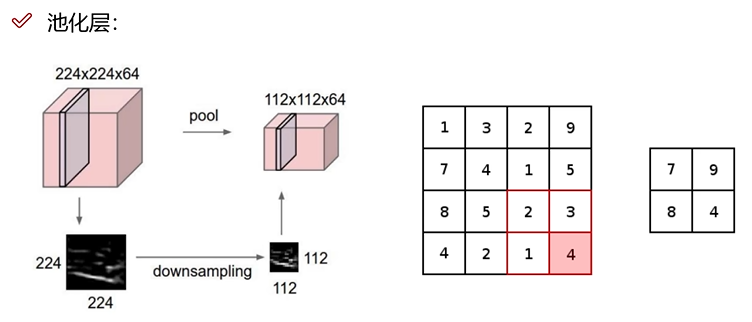
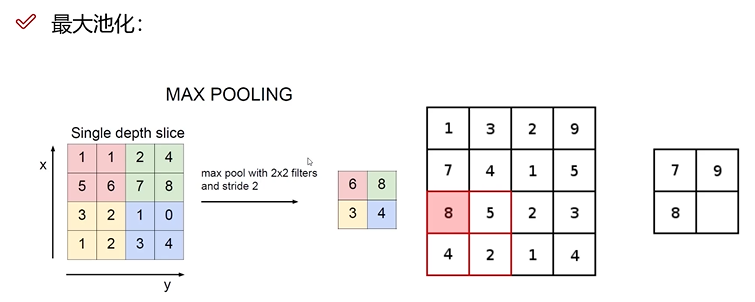
池化层
效果:卷积一定层后,可能发生维度爆炸,利用池化层降低维度。
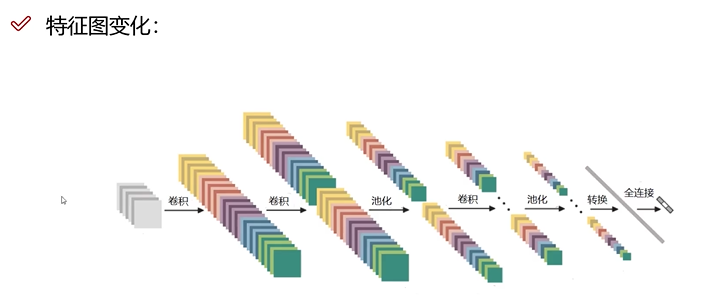
特征图变化
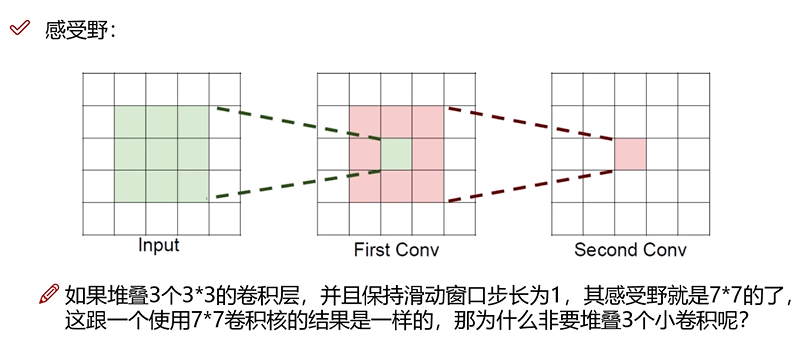
感受野
可以看到,到第二个卷积层后,一个像素块已经感受到了周围像素块的关联性。
(可跳过)下面的经典网络只是学习时候遇见,罗列在此。
经典网络
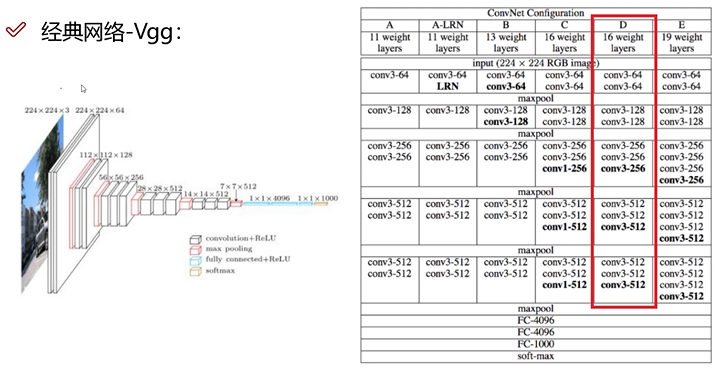
VGG
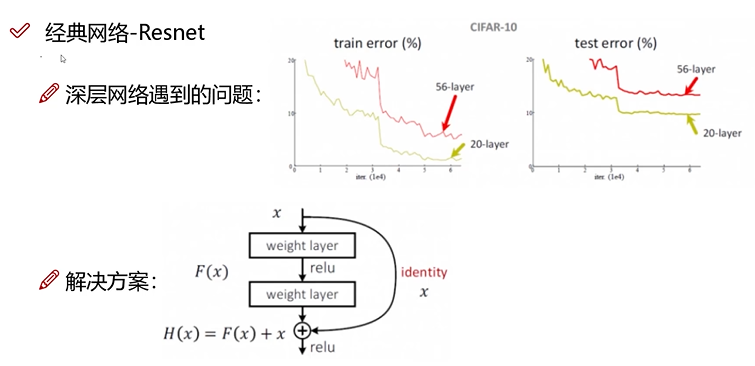
Resnet 残差网络
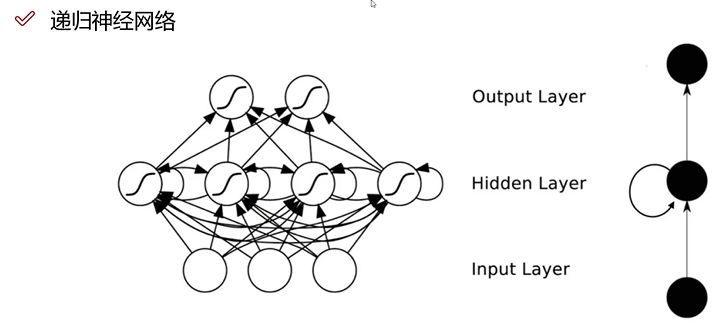
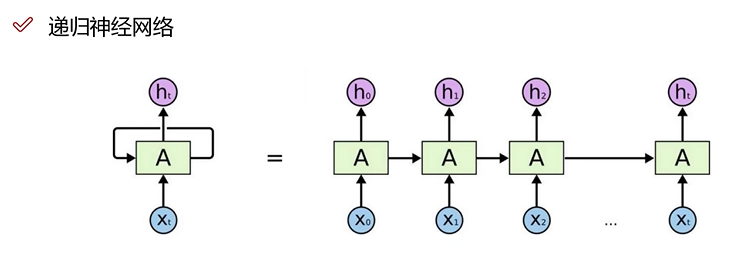
递归神经网络
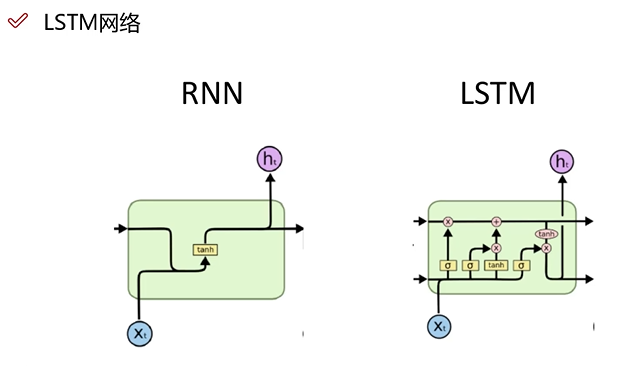
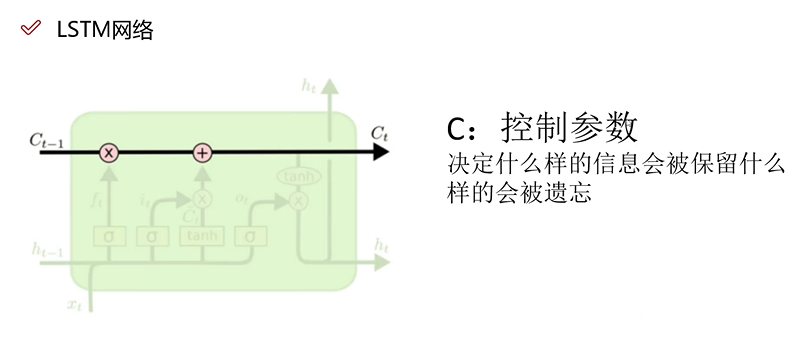
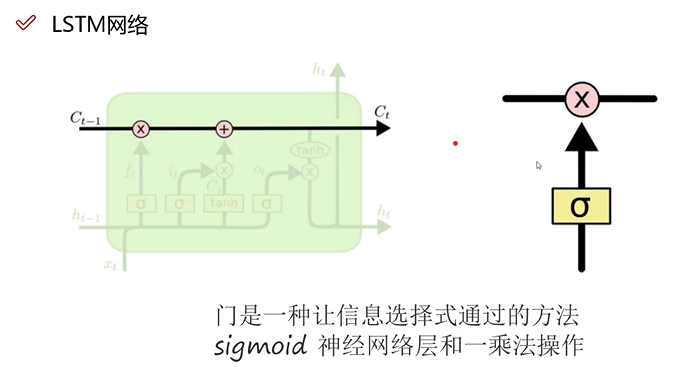
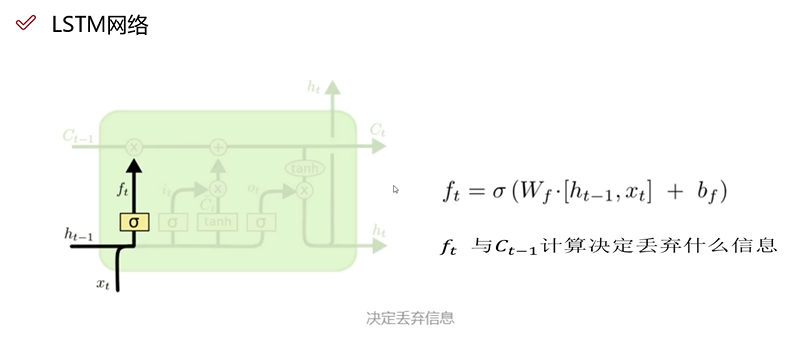
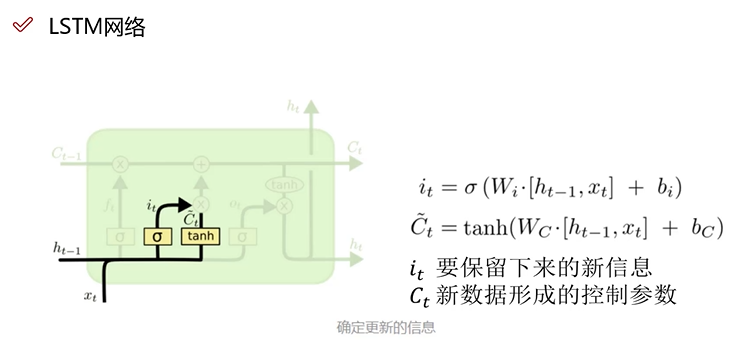
LSTM