Instant-ngp
Instant-ngp 项目主页:Instant Neural Graphics Primitives with a Multiresolution Hash Encoding
CUDA 版本:NVlabs/instant-ngp: Instant neural graphics primitives
Pytorch 版本:ashawkey/torch-ngp: A pytorch CUDA extension implementation of instant-ngp (sdf and nerf)
Motivation
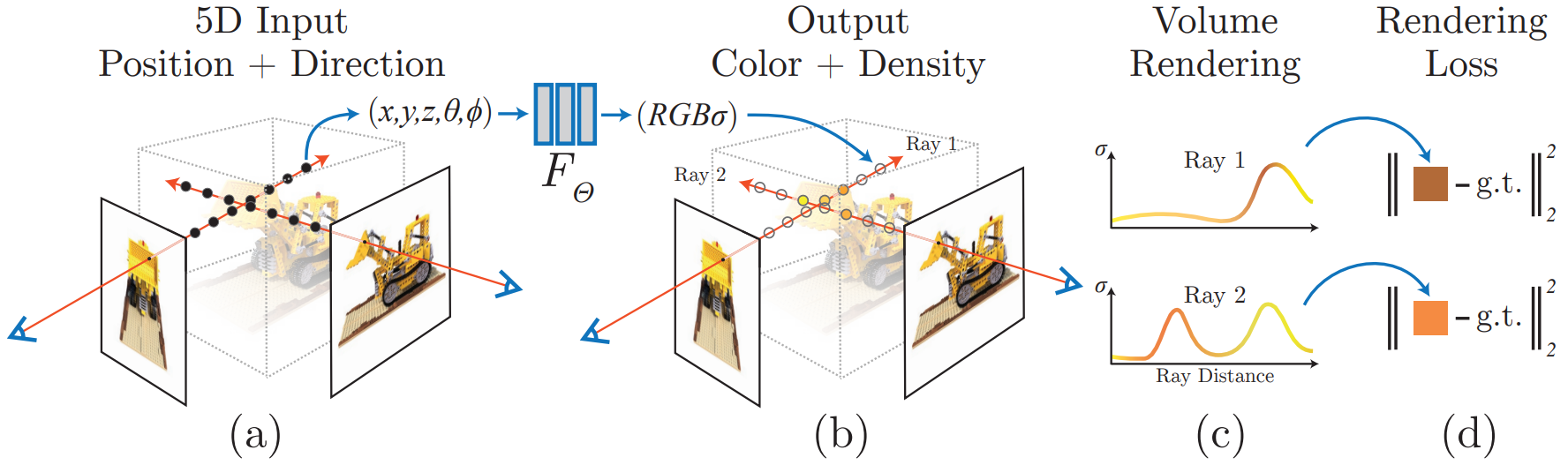
- 本文目的:NeRF 加速;
- 由 MLP 表示的 shape 和辐射场,依赖于 heuristics and structural modifications,会使训练过程更复杂,仅限制于具体的某一任务,GPU 训 练成本高昂;
- 现有的编码方式或所需内存较大、或计算成本更高,逼近效果较差;
- 密集的网络两种浪费:其一分配给空白区域的特征与表面附近的数量一样多,其二自然场景的光滑性促使多分辨率分解。
Contribution
- 通过一种通用的多分辨率 Hash 编码降低运算代价(减少浮点数和内存访问量),自适应、高效、独立
- 不依赖于任何空间数据结构、训练期间的渐进式修剪或编码场景几何的先验知识
- 利用随机梯度进行优化
- 基于多分辨率结构允许网络消除 Hash 冲突
- 整个系统利用 tiny-cuda-nn 框架的 fast fully-fused CUDA kernels,最大限度地减少带宽的浪费与计算操作,实现高效率的并行化
Multiresolution Hash Encoding
- 全连接神经网络:$m(\mathbf{y},\Phi)$
- 对输入的编码:$\mathbf{y}=ennc(\mathbf{x},\theta)$
- 可训练编码参数:$\theta$
- 可训练网络权重参数:$\Phi$
- 对输入的编码:$\mathbf{y}=ennc(\mathbf{x},\theta)$
上述可训练参数被排列成 $L$ 个级别(level),每个级别包含多达 $T$ 个维度为 $F$ 的特征向量。其中这些超参数的较为典型值设定如下:

|
Hash Encoding
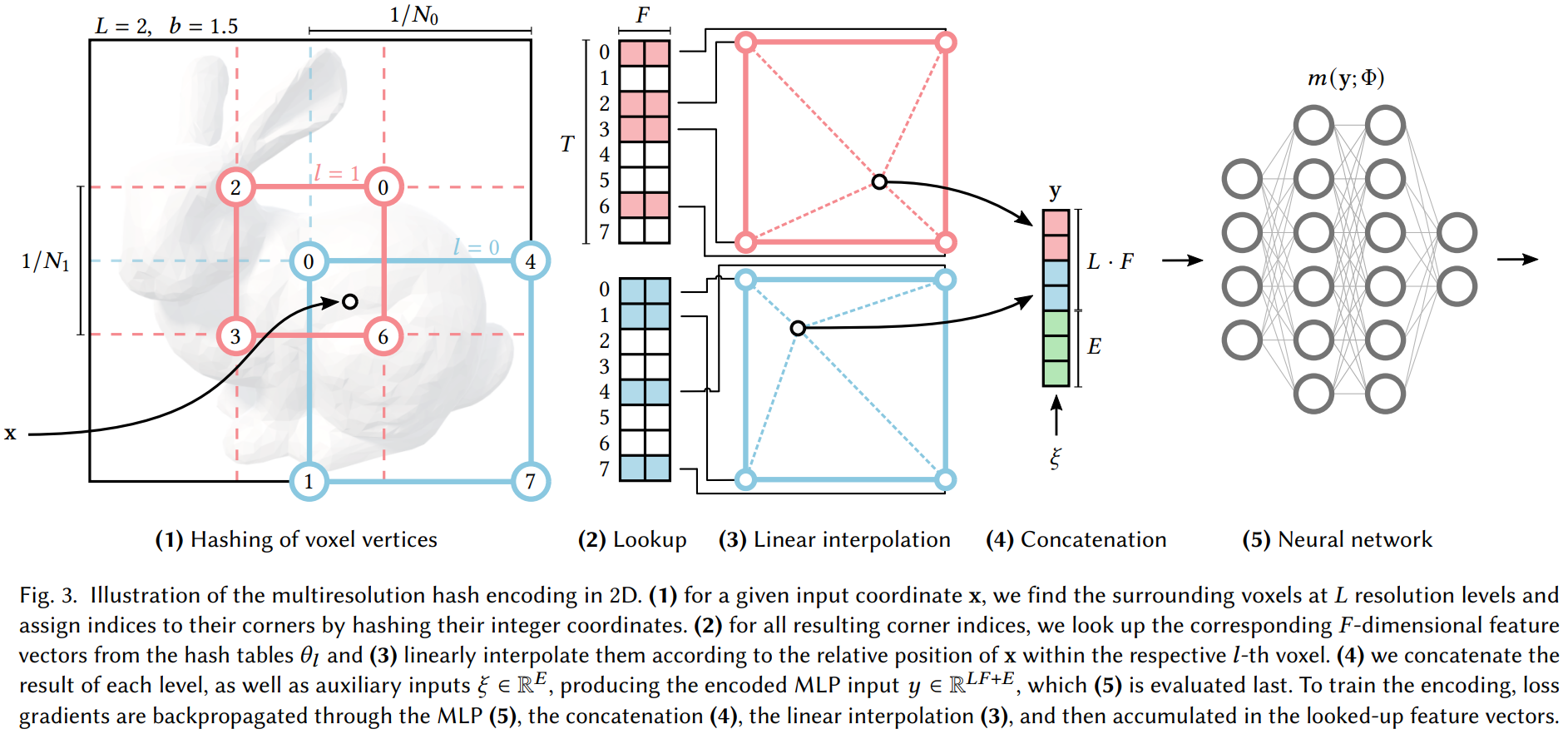
下图展示说明了多分辨率 Hash 编码的执行步骤:
|
每个级别(上图中显示的红色和蓝色)都是独立的,并且在概念上是将特征向量存储在网格的顶点处,其分辨率被选择为介于最粗略和最精细网格分辨率之间的几何级数:
$N_{max}$ 的选择是为了匹配训练数据中最精细的细节。由于级别 $L$ 的数量很大,因此生长因子通常很小。论文中用例为 $b\in[1.38,2]$。
首先考虑一个单独的级别(level)$l$ 。输入坐标 $\mathbf{x}\in\mathbb{R}^d,(d=2,3)$,在向下和向上舍入之前,按这个级别下的网格分辨率缩放:
$\lfloor \mathbf{x}_l\rfloor$ 和 $\lceil \mathbf{x}_l \rceil$ 在 $\mathbb{Z}^d$ 中横跨了一个具有 $2^d$ 个整数顶点的体素。我们将每个角(corner)映射到 level 中各自特征向量数组中的一个条目,该数组的固定大小最多为 $T$。对于粗略级别,一个密集网格需要少于 $T$ 个参数,即$(N_l)^d\leq T$,此映射为 $1:1$ 的。 在更精细的级别上,我们使用哈希函数 $h:\mathbb{Z}^d\to\mathbb{Z}_T$ 来索引数组,尽管没有显式的冲突处理,但是我们有效地可以将其视为哈希表。 相反,我们依靠基于梯度(gradient-based)优化以在数组中存储适当的稀疏细节,以及之后的神经网络 $m(\mathbf{y};\Phi)$ 来解决冲突问题。因此,可训练的编码参数 $\theta$ 的数量为$O(T)$,并以 $T\cdot L\cdot F$ 为界,在论文例子中,$T\cdot L\cdot F$ 始终为 $T\cdot 32$(见表 1)。
我们使用以下形式的哈希函数:
其中 $\bigoplus$ 表示按位异或运算(the bit-wise XOR),$\pi_i$ 是唯一的、大素数。实际上,该公式对每个维度的线性同余(伪随机)置换的结果进行异或运算,从而消除了维度对哈希值的影响。值得注意的是,为了实现(伪)独立性,只需置换 $d$ 维中的 $d-1$ 个,因此我们选择 $\pi_1:=1,\pi_2=2654435761,\pi_3=805459861$ 以获得更好的缓存一致性。
最后,根据 $\mathbf{x}$ 在其超立方体内的相对位置,对每个角的特征向量进行 $d$ 线性插值,插值权重为 $\mathbf{w}_l:=\mathbf{x}_l-\lfloor\mathbf{x}_l\rfloor$。
回想一下,这个过程对于 $L$ 个 level 都是独立进行的。每个 level 的插值特征向量,以及辅助输入 $\xi\in\mathbb{R}^E$(如编码的视图方向和神经辐射缓存中的纹理),被连接起来产生 $\mathbf{y}\in\mathbb{R}^{L F+E}$,构成 MLP $m(\mathbf{y};\Phi)$ 的编码输入$enc(\mathbf{x};\theta)$。
所以,整个 Hash 编码流程如下:
- 对于给定的输入坐标 $\mathbf{x}\in\mathbb{R}^d$,找到 $L$ 个分辨率级别下的周围体素,并通过 Hash 整数坐标为它们的 corner 分配索引;
- 对于得到的所有 corner 索引,从哈希表 $\theta_l$ 中查找相应的 $F$ 维特征向量;
- 根据 $\mathbf{x}$ 在对应第 $l$ 个体素内的相对位置对它们进行线性插值;
- 连接每个级别的结果以及辅助输入的 $\xi\in\mathbb{R}^{E}$,产生编码的 MLP 的输入 $\mathbf{y}\in\mathbb{R}^{L F+E}$;
- MLP 评估。
注:为了训练编码,损失梯度通过 MLP (5)、连接 (4)、线性插值 (3) 反向传播,然后在查找的特征向量中累积。
Performance vs. quality
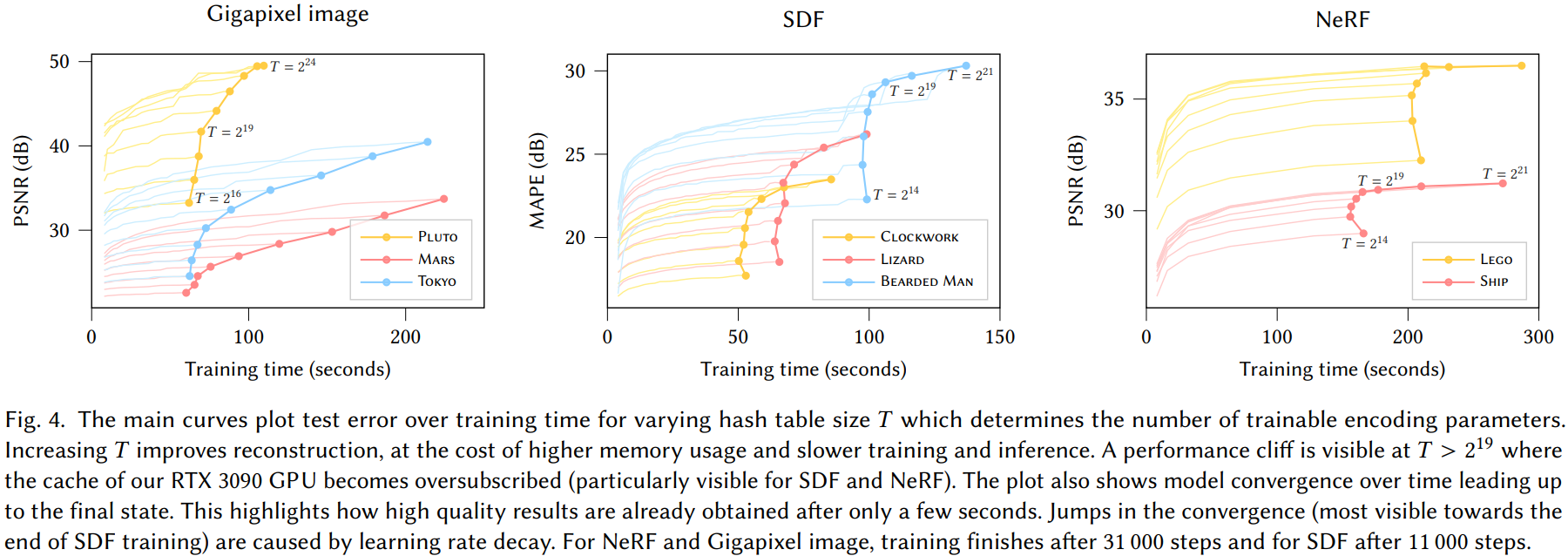
哈希表大小 $T$ 的选择可以对性能、内存和质量之间进行权衡。$T$ 值越高,质量越高,性能越低。 内存占用在 $T$ 中是线性的,而质量和性能往往呈次线性增加。我们在图 4 中分析了 $T$ 的影响,其中报告了三个神经图形基元的各种 $T$ 值的测试误差与训练时间的关系。建议使用者调整 $T$ 以将编码调整为想要的性能特征。
|
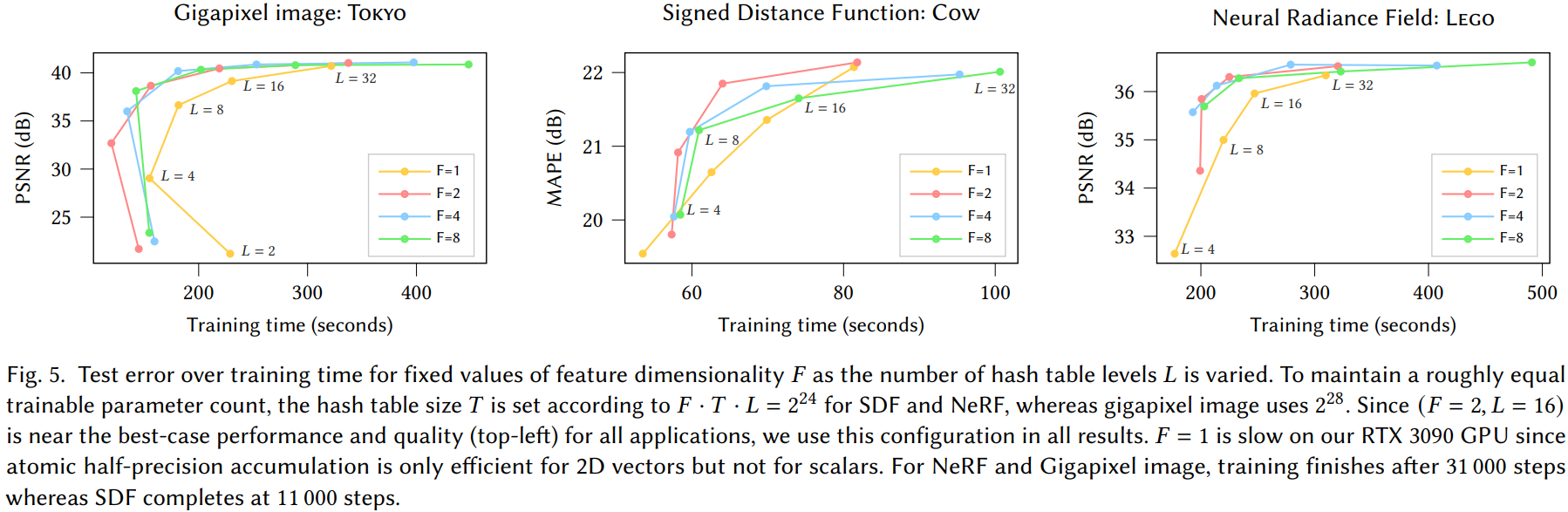
超参数 $L$(层数)和 $F$(特征维数)也权衡了质量和性能,图 5 中分析了一个近似恒定数量的可训练编码参数 $\theta$。在此分析中,发现($F=2,L=16$)在论文所有的应用程序中都是一个有利的 Pareto 最优值,因此我们在所有其他结果中使用这些值并将它们作为默认值推荐给从业者。
|
Implicit hash collision resolution
Hash 编码能够在存在哈希冲突的情况下仍然忠实地重建场景。这似乎违反直觉,但其成功的关键在于不同的分辨率层级具有相辅相成的不同优势。
- 对于粗略的层级,Hash 编码是作为一个整体的编码,是单射的——也就是说,它们根本没有冲突。 但是,它们只能表示场景的低分辨率版本,因为其特征是从较宽间隔的点网格中线性插值的。
- 精细级别由于其精细的网格分辨率可以捕获细节(高频)特征,但会遭受许多冲突——即哈希函数将不同点映射到同一个表条目上。附近具有相等整数坐标 $\lfloor\mathbf{x}_l\rfloor$ 的输入不被视为冲突;当不同的整数坐标哈希映射到相同的索引时才视为发生冲突。幸运的是,这样的冲突是伪随机分散在空间中的,并且在统计上不太可能同时发生在单个给定点的每个层级中。
当训练样本以上述方式冲突时,它们相应的梯度会平均。考虑到此类样本对最终重建的重要性很少相等。例如,辐射场中可见表面上的一个点将对重建图像有很大的贡献(具有高可见性和高密度,这两项都会成倍地影响反向传播梯度的大小),将导致其表条目发生较大变化;而空白空间中恰好引用同一条目的点将具有更小的权重。结果,更重要样本点的梯度支配了冲突平均值,并且有问题的表中条目自然会以反映更高权重点的需求的方式进行优化;然后,不太重要的点将通过多分辨率层次结构中的其他级别对其最终输出进行校正。
哈希编码的多分辨率方面涵盖了从保证无碰撞的粗分辨率 $𝑁_{min}$ 到任务所需的最精细分辨率 $𝑁_{max}$ 的全部范围。因此,它保证包括所有可以进行有意义学习的尺度,而不管稀疏性如何。 几何缩放允许仅用 $\mathcal{O}(log(N_{max}/N_{min}))$ 个层级覆盖这些尺度,这允许为 $𝑁_{max}$ 选择一个保守的大值。
Online adaptivity
注意,如果输入 $\mathbf{x}$ 的分布在训练期间随时间变化,例如,如果它们集中在一个小区域中,那么更精细的网格层级将经历更少的冲突,并且可以学习更准确的函数。换句话说,多分辨率哈希编码自动适应训练数据分布,继承了基于树的编码的优点,而无需维护可能导致训练期间离散跳跃的特定任务数据结构。其中一个应用程序,第 5.3 节中的神经辐射缓存(neural radiance caching),不断适应动画视点和 3D 内容,极大地受益于此功能。
𝑑-linear interpolation
对查询的哈希表条目进行插值可确保编码 $enc(\mathbf{x};\theta)$ 以及通过链式法则与神经网络 $m(enc(\mathbf{x};\theta);\Phi)$ 的组合是连续的。如果没有插值,网络输出中将出现网格对齐的不连续性(grid-aligned discontinuities),这将导致不希望的块状外观。 人们可能需要更高阶的平滑度,例如在逼近偏微分方程时。 计算机图形学中的一个具体示例是有符号距离函数(SDF,signed distance functions),在这种情况下,梯度 $\partial m(enc(\mathbf{x};\theta);\Phi)/\partial \mathbf{x}$,即表面法线,在理想情况下也是连续的。对于这种情况,我们在附录 A 中提供了一种低成本的方法。
Implementation
为了演示多分辨率哈希编码的速度,论文在 CUDA 中实现,并将其与 tiny-cuda-nn 框架的 fast fully-fused 的 MLP 集成。
$\mathbf{Performance\ considerations.}$ 为了优化推理和反向传播性能,以半精度(每个条目 2 个字节)存储哈希表条目。并且还维护了一个全精度参数的主副本(a master copy),以实现稳定的混合精度参数更新。
为了优化使用 GPU 的缓存,逐级评估哈希表:在处理一批输入位置时,我们安排计算查找所有输入的第一级多分辨率哈希编码,然后再查找所有输入的第二级,以此类推。因此,在任何给定时间,只有少量连续的哈希表必须驻留在缓存中,具体取决于 GPU 上可用的并行度。重要的是,这种计算结构自动充分利用了可用缓存和并行性,适用于各种哈希表大小 $T$。
在我们的硬件上,只要哈希表大小保持在 $T\leq2^{19}$ 以下,编码的性能就会大致保持不变。超过这个阈值,性能就会开始显着下降;请参见图 4。这可以通过我们的 NVIDIA RTX 3090 GPU 的 6 MB L2 cache 来解释,当 $2\cdot T\cdot F>6\cdot 2^{20}$ 时,对于单个哈希表层级来说它就太小了(其中 $2$ 是半精度条目的大小)。
每次查找的最佳特征维度 $F$ 的数量取决于 GPU 架构。 一方面,在前面提到的流式处理方法中只有少数有利于缓存局部性;但另一方面,较大的 $F$ 通过允许 F-wide 向量加载指令有利于内存一致性。$F=2$ 为我们的 GPU 提供了最佳的成本质量权衡,我们在所有实验中都使用它; 见图 5。
$\mathbf{MLP\ architecture.}$ 在所有任务中,除了我们稍后将描述的 NeRF之外,我们使用具有两个隐藏层的 MLP,这些隐藏层的宽度为 64 个神经元和校正线性单元(ReLU,rectified linear unit)激活函数,以及一个线性输出层。对于 NeRF 和 SDF,最大分辨率 $N_{max}$ 设置为 $2048\times$ 场景大小,十亿像素图像宽度的一半,在辐射缓存(radiance caching)中设置为 $219$(大值以支持扩展场景中的近距离物体)。
$\mathbf{Initialization.}$ 我们根据 Glorot 和 Bengio 初始化神经网络权重,以提供合理的激活缩放比例及其在整个神经网络层中的梯度。 我们使用均匀分布 $\mathcal{U}(-10^{-4},10^{-4})$ 初始化哈希表条目以提供少量随机性,同时鼓励初始预测接近于零。 这种初始化在我们所有的任务中都运行良好。 我们还尝试了各种不同的分布,包括零初始化,所有这些都会导致初始收敛速度稍微差一些。 散列表似乎对初始化方案具有鲁棒性。
$\mathbf{Training.}$ 我们通过应用 Adam 优化器联合训练神经网络权重和哈希表条目,其中我们设置 $\beta_1=0.9$,$\beta_2=0.99$,$\epsilon=10^{-15}$。$\beta_1$ 和 $\beta_2$ 的选择只有很小的差别,但是当它们的梯度稀疏并且很弱时,$\epsilon=10^{-15}$ 的小值可以显著加速哈希表条目的收敛。为了防止长时间训练后出现发散,我们将弱 $L_2$ 正则化(因子 $10^{-6}$)应用于神经网络权重,而没有应用在哈希表条目上。
在拟合十亿像素图片或 NeRF 时,使用 $\mathcal{L}^2$ 损失。对于 SDF,使用平均绝对百分比误差(MAPE,mean absolute percentage error),$|prediction-target|/(|target|+0.01)$,对于神经辐射缓存,使用亮度相关的(luminance-relative) $\mathcal{L}^2$ 损失。
我们观察到最快的收敛速度下,符号距离函数的学习率为 $10^{−4}$,否则为 $10^{−2}$,神经辐射缓存的批处理大小为 $2^{14}$,否则为 $2^{18}$。
最后,对于梯度正好为 $0$ 的哈希表条目,我们跳过 Adam 步骤。这在梯度稀疏时节省了$\sim 10\%$的性能,这在 $T\gg BatchSize$ 时很常见。尽管这种启发式违反了 Adam 背后的一些假设,但我们观察到收敛性没有下降。
$\mathbf{Non-spatial\ input\ dimensions}\ \xi\in\mathbb{R}^E.$ 多分辨率哈希编码的目标是具有相对较低维度的空间坐标。我们所有的实验都是在 2D 或 3D 中进行的。 然而,在学习光场时,将辅助维度 $\xi\in\mathbb{R}^E$ 输入到神经网络中通常很有用,例如观察方向和材料参数。在这种情况下,可以使用已建立的技术对辅助维度进行编码,其成本不会随维度超线性增加;我们在神经辐射缓存中使用 one-blob 编码,在 NeRF 中使用球谐波基,类似于并发工作。