体渲染相关知识
体渲染相对于表面渲染优势
表面渲染和体渲染技术上最核心的区别在于:光线是否会在物体内部发生作用。体渲染会考虑光线在物体内部的传播,表面渲染的光线仅仅在物体表面发生作用。这导致的核心应用区别是:表面渲染只适合于渲染漫反射材质、金属材质、塑料材质、镜面材质等。但对于玉石、烟雾等半透明材质,只有可微体渲染才能支持。同时,体渲染的渲染代价要高于表面渲染。
体素
每一个体素都代表着空间中的一个单位,尽管可以把体素想象成一个很小的立方体,但更应该把每个体素认为是从连续的三维信号中对一个无穷小的点采样得到的样本。我们关注的体渲染一般可以理解为:刻画空间中每个体素的密度与颜色值。
体渲染积分
最基础的、也是我们最常用的体渲染算法是 Ray-Casting 算法,这是一种逐像素的直接体渲染算法:对要渲染的图片中的每一个像素,从眼睛发出一束光线,传过像素中心,进入体内部,然后对沿着射线遇到的体密度进行光学属性的积分(数值)。注意到,这种通用的描述假定了体和映射到体上的光学属性是连续的。在实际中,体素是离散的,并且积分的计算结果是数值近似的。
- 对于一条光线 $\mathbf{x}(t)=\mathbf{o}+t\mathbf{v}\in\mathbb{R}^3$,$\mathbf{o}$ 为光线的原点,$\mathbf{v}$ 为光线的方向,利用距离 $t$ 进行参数化;
- 对沿光线的某个位置对应的标量,记为 $s(\mathbf{x}(t))\in\mathbb{R}$,常用的比如体密度、深度;
- 光线吸收系数 $k(t)=k(s(\mathbf{x}(t)))$;
- 辐射颜色 $c(t)=c(s(\mathbf{x}(t)))$;
常用的光照模型认为粒子会发光,也会遮挡(吸收)到来的光,但是没有散射或间接光。所以此时体渲染方程即对吸收系数 $k(t)$、辐射颜色 $c(t)$ 沿着光线进行积分,即得某位置上单个粒子到达渲染图片的颜色为:
当考虑到这条射线上所有可能位置 $t$ 发出的辐射总和,即有最终渲染:
离散化上述积分:
实际上,体渲染积分是通过以从前到后或从后到前的 Alpha混合(合成) 的方式来近似求解的。(下述记号是以均匀采样标写的,所以 $\deltai=t{i+1}-t_i=\Delta t$)
- 累积透射度 $T(t)=e^{-\int_0^t k(y)dy}$,离散情形 $T_i=e^{-\sum_j k(j\cdot\Delta t)\Delta t}$;
- 累积不透明度 $A(t)=1-T(t)$,离散情形 $A_i=1-T_i$;
- 辐射颜色离散 $c_i=c(t_i)\Delta t$;
此时最终辐射总和计算为:
上述这个公式能通过以从后到前或从前到后的顺序的 Alpha混合(合成) 来迭代计算。
Alpha合成
上述那个公式能通过以从后到前使用 $n-1$ 到 $0$ 的 $i$ 来迭代计算:
新值 $Ci^\prime$ 可以由当前位置 $i$ 的颜色 $C_i$ 和不透明度 $A_i$ 以及前一个位置 $i+1$ 的复合颜色 $C{i+1}^\prime$ 来算出。起始条件是 $C_n^\prime=0$。
- 注意到,在所有混合方程中,我们使用带有不透明度权重的颜色,也就是所说的
associated colors。带有不透明度权重的颜色是已经提前乘好他们相关的不透明度的颜色。这是一种十分便利的符号,在用于插值时尤其重要。可以证明,对颜色和不透明度分别进行插值后会造成失真,但对不透明度加权的颜色进行插值就会得到正确的结果。
下面是可选的从前到后顺序的迭代公式,$i$ 从 $1$ 递增至 $n$:
新值 $Ci^\prime,A_i^\prime$ 可以由当前位置 $i$ 的颜色 $C_i$ 和不透明度 $A_i$ 以及前一个位置 $i-1$ 的复合颜色 $C{i-1}^\prime$ 和不透明度 $A_{i-1}^\prime$ 来算出。起始条件是 $C_0^\prime=0,A^\prime_0=0$。
- 注意到从前到后复合需要追踪
alpha的值,然而从后到前组合不需要。在硬件实现中,使用从前到后的复合的话,意味着终点alpha必须被帧缓冲所支持(比如一个alpha的值必须存在帧缓冲中,然后它必须能在混合操作中用作乘数)。然而,由于从前到后复合的主要优点是一种叫做提前射线终止的常见优化方法,这种方法会在沿射线累计的alpha到达 $0$ 时,将过程立刻终止。这在硬件上是难以执行的,使用 GPU 的体渲染通常使用从后到前的复合。
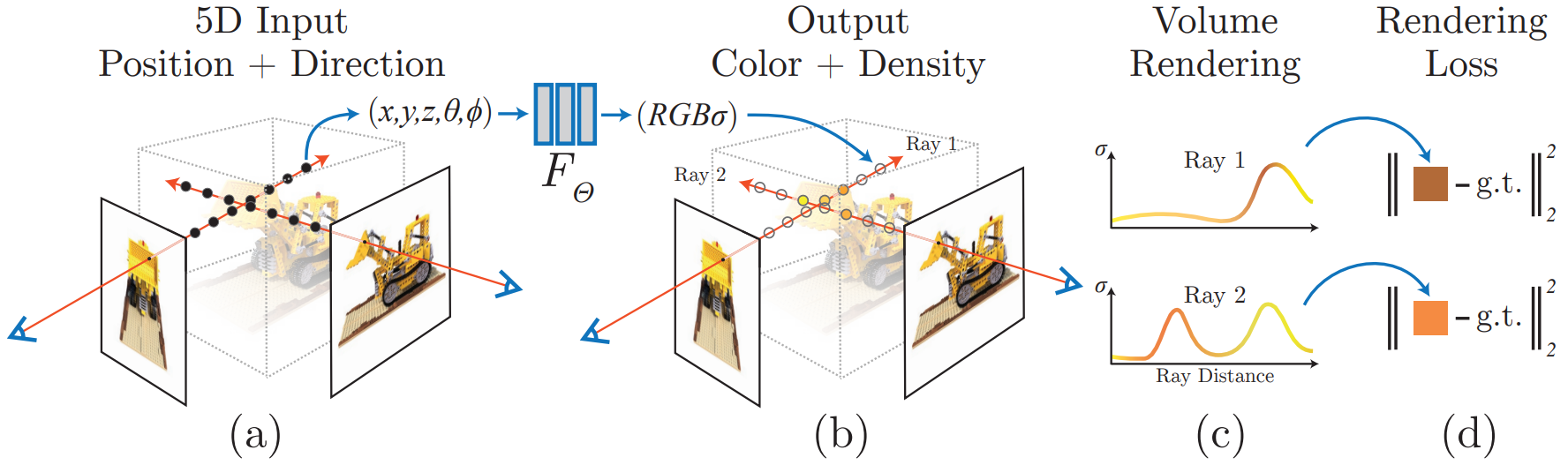
NeRF中的体渲染
(综合 NeRF 原文和其他论文中的理解)
我们考虑恢复体素的颜色与密度:
- 体密度 $\sigma(\mathbf{x}(t))$;
- 累积透射度 $T(t)=e^{-\int_0^t\sigma(\mathbf{x}(y))dy}$;
- 累积不透明度 $A(t)=1-T(t)$,将 $A(t)$ 看作是一个累积分布函数;
- 概率密度函数(PDF)$\tau(t)=\frac{d T(t)}{d t}=\sigma(\mathbf{x}(t))T(t)$;
从而最终合成颜色为: